<<Предыдущая
страница
В.
А. Ассонова, Н.
В. Ассонова
Раздел
1.
Задачи
на
построение
Глава
3. ЭТАП
ИССЛЕДОВАНИЯ
В РЕШЕНИИ
ЗАДАЧ НА
ПОСТРОЕНИЕ
Этап
исследования
завершает
решение,
выясняет все
его случаи,
обеспечивает
полноту
решения.
Необходимо
определить
цель
исследования,
его идею и
принципы и
указать
основные
моменты
исследования.
§ 1.8. Цель,
принципы и
основные
моменты
исследования
в задачах на
построение
Решение
задачи на
построение
может
считаться
законченным,
если будут
разрешены
три вопроса:
1)
при
всяком ли
выборе
данных
элементов
задача имеет
решение;
2)
при
каком выборе,
в частности,
она не имеет
решения и
3)
при
каком выборе
данных
задача имеет
решения и
сколько.
На эти три
вопроса
должно
ответить
исследование
задачи.
Отсюда
следует цель
исследования:
установить,
какие могут
существовать
для данных
элементов
соотношения
или взаимные
положения,
при которых (разрешимая
при помощи
указанных
средств
построения)
задача не
имеет ни
одного
решения;
имеет одно
или
несколько (и
сколько
именно)
решений;
имеет
бесконечное
множество
решений.
При этом
понимается,
что
выяснение
поставленных
вопросов
осуществляется
геометрическим
путем.
Требуемые
соотношения
мыслятся не
обязательно
аналитическими.
Аналитический
ответ
желателен, но
принципиально
в области
геометрических
построений
не необходим.
Поэтому в
дальнейшем
нас будет в
основном
интересовать
геометрическая
сторона
исследования,
геометрические
его
результаты,
хотя в
качестве
примеров и
будет
приводиться
аналитическое
выражение
результатов
исследования.
Переходим к
установлению
идеи
исследования.
Идея
исследования
в решении
задачи на
построение
должна
подчеркивать
его
геометрический
характер и
вытекать из
идеи анализа.
Только
идейная
связь этапов
анализа,
построения и
исследования
приведет к
завершению
решения и
достижению
цели
исследования.
 Нами
выбрана в
качестве
руководящей
в анализе
идея
отыскания
так
называемых
искомых
элементов (точек)
фигуры по их
свойствам и
отнесение
элемента
двум
геометрическим
образам.
Отсюда
следует
самое общее
выражение
идеи
исследования:
выяснение
всех
характерных,
отвечающих
задаче
случаев
взаимного
расположения
двух
геометрических
образов, к
которым
принадлежит
искомый
элемент
Нами
выбрана в
качестве
руководящей
в анализе
идея
отыскания
так
называемых
искомых
элементов (точек)
фигуры по их
свойствам и
отнесение
элемента
двум
геометрическим
образам.
Отсюда
следует
самое общее
выражение
идеи
исследования:
выяснение
всех
характерных,
отвечающих
задаче
случаев
взаимного
расположения
двух
геометрических
образов, к
которым
принадлежит
искомый
элемент
Поскольку
конкретное
разыскание
таких общих
точек
осуществлено
уже на этапе
построения,
то отсюда
следует, что
один из
случаев,
ожидаемых в
исследовании,
уже
рассмотрен
при
построении.
Само
построение
дает
возможность
указать
геометрический
прием
исследования.
В самом деле,
какое-то из
геометрических
мест всегда
строится
последним.
Это
геометрическое
место
определяется
в конце
концов
данными
элементами.
Очевидно, что,
варьируя
некоторые
данные, мы
сможем
получить все
различные
случаи
наличия или
отсутствия
точек, общих
геометрическим
местам.
Рассмотрим
в качестве
примера
метрическую
задачу 3: построить
треугольник
по а, b и В (см.
анализ
задачи в §2).
Удобно
считать, что
последним в
этой задаче
строится
геометрическое
место (С,
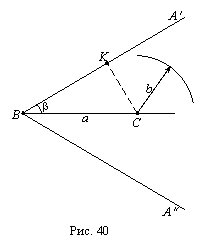
b). Это
геометрическое
место (рис. 40)
определяется
двумя
элементами:
центром С
(конец
данного
отрезка а)
и радиусом b (b
данный
отрезок).
Достаточно
варьировать,
например, b,
чтобы
получить все
возможные
случаи
взаимного
расположения
геометрических
мест (С, b)
и луча ВА’,
наклоненного
под углом b
к отрезку а.
Этот
изменяемый
нами данный
элемент
назовем параметром
исследования.
В данном
примере
параметром
является
отрезок b.
Мы могли бы
выбрать в
качестве
параметра
отрезок а. Это было
бы в случае,
когда в
анализе
искомой
оказалась
вершина В,
которую
можно было
отыскать как
точку
пересечения
дуги
сегмента,
построенного
на отрезке b
и вмещающего
угол b,
и окружности (С,
а). Можно было
бы выбрать в
качестве
параметра
исследования
в этой задаче
и угол В.
Ход анализа и
построения
существенно
определяют
выбор
параметра.
Поэтому, если
окажется, что
этот выбор
чем-либо не
удобен для
исследования,
приходится
обращаться к
иному
варианту
анализа.
Таким
образом, в
качестве
параметра
может быть
выбран любой
элемент из
данных.
Однако
множество
вариаций
параметра
бесконечно, и
необходимо
указать
какие-то
вполне
определенные
границы
варьирования
параметра.
Так, в
рассматриваемой
задаче в
бесконечном
множестве
вариаций
параметра b
существенно
различны
такие его
состояния:
b
< CK, b=CK,
CK < b < a, b=a,
a < b.
Это и дает,
соответственно,
пять
существенно
различных
случаев
взаимного
расположения
двух
геометрических
мест:
окружности (С,
b)
и луча ВА’,
наклоненного
к отрезку а под углом b. Эти случаи
изображены
на рисунке 41.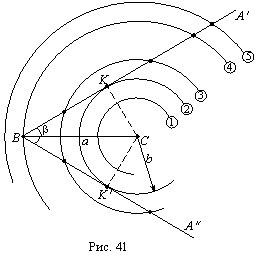 Границы
изменения
параметра
выявляются в
ходе
исследования,
когда
графически,
путем
испытаний, мы
стараемся
получить все
новые
характерные
случаи
взаимного
расположения
интересующих
нас
геометрических
мест.
Некоторые
элементы
чертежа для
исследования
помогают
быстрее
установить
эти случаи. В
рассматриваемом
примере
такими
элементами
будут
отрезки ВС=а
и КС=аsinb.
Отрезки ВС
и КС и
определяют
характерные
значения
параметра,
переходя
через
которые
параметр
дает новый
случай
исследования.
Границы
изменения
параметра
выявляются в
ходе
исследования,
когда
графически,
путем
испытаний, мы
стараемся
получить все
новые
характерные
случаи
взаимного
расположения
интересующих
нас
геометрических
мест.
Некоторые
элементы
чертежа для
исследования
помогают
быстрее
установить
эти случаи. В
рассматриваемом
примере
такими
элементами
будут
отрезки ВС=а
и КС=аsinb.
Отрезки ВС
и КС и
определяют
характерные
значения
параметра,
переходя
через
которые
параметр
дает новый
случай
исследования.
Элементы
чертежа,
позволяющие
уточнить
границы
изменения
параметра,
дающие его
характерные
значения, мы
назовем
критическими
элементами.
В нашем
примере это
отрезки ВС
и КС.
Если
параметр
угол, то и
критические
элементы
суть углы.
Исходя из
сказанного,
мы
сформулируем
первый
принцип исследования
в
метрических
задачах.
Существование
решения
зависит,
вообще
говоря, от
существования
точек, общих
геометрическим
местам,
содержащих
искомый
элемент.
Существование
таких общих
точек
устанавливается
графически
при помощи
изменения
какого-нибудь
одного из
данных
элементов
параметра,
характерные
значения
которого
определяются
при помощи
так
называемых
критических
элементов.
Вообще
говоря, этот
принцип
можно
распространить
на задачи
положения,
однако тогда
пришлось бы
очень часто
вводить
новые
элементы,
явно не
указанные в
условии
задачи,
косвенно
выбирать
параметр и
критические
элементы. Вот
почему для
задач
положения мы
будем
непосредственно
применять
идею
исследования:
меняя
взаимное
расположение
данных
геометрических
образов, т. е.
варьируя
чертеж-задание,
будем
стараться
получить все
возможные
характерные
случаи
взаимного
расположения
геометрических
мест,
содержащих
искомый
элемент.
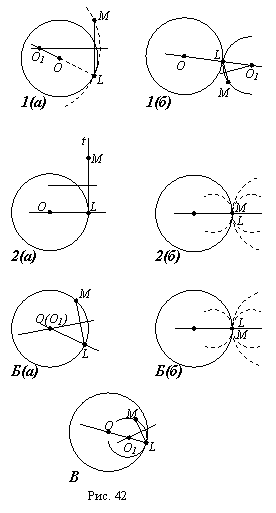
Так, в
задаче 4: построить
окружность,
проходящую
через данную
точку М и
касающуюся
данной
окружности О
в данной ее
точке L
(см. §2),
варьируя
взаимное
расположение
данных, легко
установить
такие случаи (рис.
42):
А) Точка М
вне
окружности w:
1) М не
принадлежит
касательной t:
а) М и
окружность w
по одну
сторону от t;
б) М и
окружность w
по разные
стороны от t;
2) М Μ
t:
а) М
не совпадает
с L; б) М
совпадает с L;
Б) Точка М
Μ
w:
а) М
не совпадает
с L; б) М
совпадает с L;
В) Точка М
внутри
окружности w.
Таким
образом,
принцип
варьирования
данных
элементов
есть первый
принцип
исследования.
Установим
далее
второй
принцип исследования
принцип
подсчета
числа
решений.
Из точек,
общих двум
геометрическим
местам, мы
отбросим те,
которые не
ведут к
построению
фигур,
удовлетворяющих
требованию
задачи.
Остальные
точки, если их
множество не
пустое, ведут
к построению
искомых
фигур. Далее
встает
вопрос о
подсчете
числа
решений.
В начале
книги было
сказано, что
все задачи на
построение
можно
разбить на
два вида:
 1)
задачи
метрические,
в которых
требуется
построить
фигуру,
имеющую
заданные
размеры и
форму, но
произвольно
расположенную
на плоскости;
в этих
задачах
фигура
отыскивается,
как говорят, «с
точностью до
положения на
плоскости»;
1)
задачи
метрические,
в которых
требуется
построить
фигуру,
имеющую
заданные
размеры и
форму, но
произвольно
расположенную
на плоскости;
в этих
задачах
фигура
отыскивается,
как говорят, «с
точностью до
положения на
плоскости»;
2) задачи
положения, в
которых
требуется
построить
фигуру,
занимающую
определенное
(относительно
других фигур)
положение на
плоскости и,
быть может,
имеющую
некоторые
элементы
заданных
размеров.
Ясно, что
вопрос о
подсчете
решений,
исходя из
наличия
точек, общих
геометрическим
местам,
должен
решаться
совершенно
различно для
задач
каждого вида.
В задачах
положения
каждая вновь
построенная
и отвечающая
условию
задачи
фигура есть
новое
решение,
отличное от
предшествующих,
хотя бы
полученная
вновь фигура
и была «равна»
предшествующим.
В задачах
метрических
для
осуществления
построения
можно
избрать
любую часть
плоскости,
поэтому
фигуру,
удовлетворяющую
условию
задачи, можно
считать
перемещаемой
в плоскости (но
не в
пространстве,
так как речь
идет о
построении в
плоскости).
Фигура
остается
одним и тем же
решением,
куда бы ее ни
сдвинуть по
плоскости.
Поэтому все
фигуры,
которые при
перемещении
в плоскости
построения
могут быть
совмещены
всеми их
точками,
означают
одно решение.
Очевидно, что
различными
решениями
будут только
те фигуры (отвечающие
условию
задачи),
которые
нельзя
совместить
друг с другом
всеми их
точками
путем
перемещения
только в
плоскости
построения.
Отсюда ясно,
что в случае
метрических
задач
подсчитывать
число
решений по
числу точек,
общих
геометрическим
местам,
вообще
говоря,
нельзя.
На
основании
сказанного
мы введем
следующий
принцип
подсчета
числа
решений (второй
принцип
исследования).
В задачах
положения
каждая
фигура,
удовлетворяющая
требованию
задачи, есть
новое
решение, если
она не
тождественна
какой-либо из
построенных.
В
метрических
задачах
фигура,
удовлетворяющая
требованию
задачи, есть
новое
решение, если
никаким
перемещением
в плоскости
построения
ее нельзя
совместить
ни с одной из
ранее
построенных
и
удовлетворяющих
условию
задачи фигур.
Из
сказанного
ранее о
свойствах
симметричных
относительно
прямой и
симметричных
относительно
точки фигур
следует, что в
метрических
задачах
всякие две
взаимно
симметричные
относительно
некоторой
прямой
фигуры,
не
обладающие
осевой
симметрией,
суть
различные
решения. Две
взаимно
симметричные
относительно
некоторой
прямой
фигуры,
имеющие ось
симметрии,
означают
одно решение.
Две фигуры,
взаимно
симметричные
относительно
точки,
означают
одно решение
и т. д.
Покажем
теперь, как
сформулированные
выше два
принципа
исследования
применяются
конкретно к
задаче.
Одновременно
мы отметим
основные
моменты
исследования,
указывающие
последовательность
осуществления
принципов
исследования
и ведущие к
достижению
его цели.
В качестве
примера
продолжим
исследование
той же
метрической
задачи: построить
треугольник
по а, В и b.
Первый
момент
исследования
подготовка
чертежа для
исследования
и указание
параметра. Пользуясь
результатами
анализа и
построения,
воспроизводим
часть
построения
на отдельном
чертеже,
стремясь
сохранить
конфигурацию,
имевшую
место в
соответствующей
части
построения (масштаб
не
соблюдается).
Например, в
рассматриваемом
случае
изображаем
основание ВС,
острый угол А’ВС
и
симметричный
ему (относительно
ВС) угол А²ВС (рис. 43). Таким
образом, из
этапа
построения
воспроизведено
одно из
геометрических
мест, при
помощи
которых
отыскивалась
искомая
точка А.
При этом
выясняется,
что отрезок b
удобно
считать
параметром.
Пользуясь
результатами
анализа и
построения,
воспроизводим
часть
построения
на отдельном
чертеже,
стремясь
сохранить
конфигурацию,
имевшую
место в
соответствующей
части
построения (масштаб
не
соблюдается).
Например, в
рассматриваемом
случае
изображаем
основание ВС,
острый угол А’ВС
и
симметричный
ему (относительно
ВС) угол А²ВС (рис. 43). Таким
образом, из
этапа
построения
воспроизведено
одно из
геометрических
мест, при
помощи
которых
отыскивалась
искомая
точка А.
При этом
выясняется,
что отрезок b
удобно
считать
параметром.
Второй
момент
исследования
графическое
установление
(при помощи
изменения
параметра)
всех
характерных
случаев
взаимного
расположения
геометрических
мест.
В нашем
примере все
характерные
различные
случаи
взаимного
расположения
геометрических
мест (С, b) и ВА’
уже получены
при помощи
изменения
отрезка b.
Целью
второго
момента
исследования
является
графическое
получение
всех
характерных
случаев
взаимного
расположения
геометрических
мест (в нашей
задаче
случаи 1, 2, 3, 4 и 5) и
указание
критических
элементов (в
нашем
примере
отрезки ВС
и СК).
Третий
момент
исследования
подсчет
числа
решений.
Выясним в
каждом
случае,
имеются ли
точки, общие
обоим
геометрическим
местам, и
какие из этих
точек
приводят к
построению
искомой
фигуры.
Устанавливаем
число
решений,
исходя из
принятого
принципа.
Записываем
результат
геометрического
исследования.
В нашей
задаче это
будет
выглядеть
так (рис. 43):
0 <
b
< 90°.
1)
b < СК
нет решений;
2)
b=СК
максимум два
решения (прямоугольный
треугольник ВКС
и ему
симметричный
относительно
ВС);
3)
СК <
b
<
ВС
максимум четыре
решения (треугольники
А1ВС, А2ВС и им
симметричные
относительно
ВС);
4)
b=
ВС одно
решение (треугольник
А3ВС
равнобедренный);
5)
ВС <
b
максимум два
решения (треугольник
А4ВС
и ему
симметричный
относительно
ВС).
Заметим, что
критические
отрезки СК
и ВС
еще не
выражены
через данные
элементы.
Кроме того,
запись
результатов
исследования
показывает,
что число
решений
может быть в
некоторых
случаях
меньшим, в
зависимости
от
соотношений
между
данными
элементами.
Поэтому
желательно
уточнить
геометрические
результаты
исследования
при помощи
аналитического
их выражения.
Это мы
сделаем в
последнем
моменте
исследования.
Четвертый
момент
аналитическое
выражение
результатов
исследования.
Выражаем
критические
элементы
через данные.
Выясняем
соотношения
между
данными, при
которых
построенные
фигуры будут
обладать
осевой
симметрией, и
уточняем
результаты
исследования
в отношении
минимума
числа
решений.
Для
рассматриваемой
задачи (0<b<90°) будем
иметь
следующее (рис.
43):
СК=а sinb,
ВС=а.
Случай
2. Если
треугольник ВСК
равнобедренный,
т. е. если b=45°
и
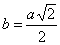 , то задача
имеет одно
решение.
, то задача
имеет одно
решение.
Случай
3. Если
треугольник А1ВС
равнобедренный,
а
треугольник А2ВС
неравнобедренный,
т. е. если а=2b cosb,
но
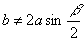 , то
задача имеет три
решения (аналогично,
в случае если
, то
задача имеет три
решения (аналогично,
в случае если
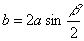 , но аΉ2b cosb,
тогда
треугольник А2ВС
равнобедренный,
а
треугольник А1ВС
неравнобедренный).
Однако
возможен
случай, когда
треугольники
А1ВС
и А2ВС
оба
равнобедренные.
Тогда задача
имеет только два
решения.
Нетрудно
подсчитать,
что это
случится при b=36° и
, но аΉ2b cosb,
тогда
треугольник А2ВС
равнобедренный,
а
треугольник А1ВС
неравнобедренный).
Однако
возможен
случай, когда
треугольники
А1ВС
и А2ВС
оба
равнобедренные.
Тогда задача
имеет только два
решения.
Нетрудно
подсчитать,
что это
случится при b=36° и
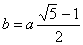 .
.
Случай
5. Если b
>
a
и a
=
2b cosb,
то задача
будет иметь одно
решение, так
как
треугольник А4ВС
будет
равнобедренный.
Теперь
можно
результаты
исследования
задачи
записать в
следующем
виде:
0 <
b
< 90°.
1)
b <
a sinb
- нет
решений;
2)
b =
a sinb
- максимум два
решения (при b
= 45°
- одно
решение);
3)
a sinb
<
b <
a
максимум четыре
решения (при a =
2b cosb
и
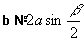 или
при a
Ή
2b cosb
и
или
при a
Ή
2b cosb
и
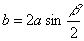 - три
решения, при
- три
решения, при
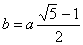 и b
= 36°
- два решения);
и b
= 36°
- два решения);
4)
b = a одно
решение;
5)
b >
a
максимум два
решения (при a =
2b cosb
-
одно
решение)
Конечно, все
эти
результаты
справедливы,
если задача
рассматривается
как
метрическая.
Несколько
иные
результаты
исследования
будут в
случае, когда b
= 90°
и при 90°
<
b
<
180°.
Закончим
исследование
в
рассматривавшейся
ранее задаче
положения (задача
4).
Исследование
здесь
заключается
в
рассмотрении
всех
возможных
случаев
взаимного
расположения
точки М
и окружности (О,
OL),
причем в
каждом
частном
случае
должно быть
указано
число
решений. Все
эти случаи
изображены
на рисунке 42, и
нам осталось
лишь
оформить
результаты
исследования.
Имеем:
1 (а) одно
решение,
окружность w1
охватывает
данную;
1 (б) одно
решение,
случай
рассмотрен в
анализе (§2);
2 (а) нет
решения;
2 (б) бесконечное
множество
решений;
Б (а) одно
решение,
окружность (О,
OL)
совпадает с
окружностью (О1,
ОМ);
Б (б) бесконечное
множество
решений;
В одно
решение,
внутреннее
касание.
Аналитически
выражать
результаты в
каждом
случае здесь
не
представляется
необходимым,
так как дано
исчерпывающее
геометрическое
исследование.
Можно
указать, что
задача не
имеет
решения в
случае, когда ОМ2 =
OL2 +
LM2
и L
не совпадает
с М.
Рассмотрим
еще одну
метрическую
задачу,
анализ в
которой
несложен, но
исследование
достаточно
громоздко.
Задача
21.
Построить
треугольник
по а, ΠА
= a
и условию, что
основание Р
высоты ha делит
отрезок а в
отношении m : n,
где m
и n
данные
отрезки.
Анализ.
Очевидно, что
искомая
вершина А, если она
существует,
является
точкой
пересечения
дуги
сегмента,
построенного
на отрезке а
и вмещающего
угол a, и прямой РА
^
ВС (рис.
44 а).
Построение
и
доказательство
не вызовут
затруднений.
Обратимся к
исследованию.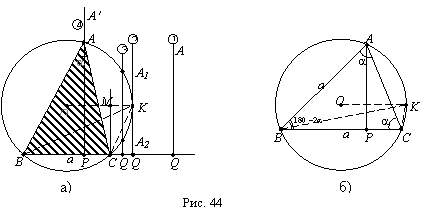 Исследование. Изображаем
на отдельном
чертеже ГМТ,
из которых
отрезок а
виден под
углом a,
точку Р
и РА ^
ВС (рис.
44 а). Замечаем,
что
существует
еще точка Q,
делящая ВС
в отношении m
: n
внешним
образом.
Изображаем QA² ^
ВС.
Исследование. Изображаем
на отдельном
чертеже ГМТ,
из которых
отрезок а
виден под
углом a,
точку Р
и РА ^
ВС (рис.
44 а). Замечаем,
что
существует
еще точка Q,
делящая ВС
в отношении m
: n
внешним
образом.
Изображаем QA² ^
ВС.
Наличие или
отсутствие
решений
зависит от
наличия или
отсутствия
точек, общих
сегменту,
построенному
на отрезке а
и вмещающему
угол a, и
перпендикуляру
РА, а
также
сегменту и
перпендикуляру
QA².
Необходимо
рассмотреть
следующие
случаи:
I.
0°
<
a
< 90°
и m Ή
n;
II.
90°
£
a
< 180°
и m Ή
n
(пусть для
определенности
в том и другом
случае m
>
n).
Случай
m =
n
мы не будем
рассматривать,
так как
очевидно, что
задача при
этом имеет
одно решение
равнобедренный
треугольник
с высотой,
равной
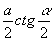 , причем
построение в
этом случае
упрощается.
, причем
построение в
этом случае
упрощается.
I.
0°
<
a
< 90°.
Рисунок 44 а
показывает
все
возможные
случаи
взаимного
расположения
дуги
сегмента и
перпендикуляров
РА’
и QA²
(для простоты
перпендикуляр
РА’
изображен в
одном
положении).
Параметром
здесь
является
отрезок CQ,
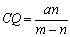 .
.
Критический
элемент
отрезок МК,
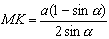 .
.
При помощи
чертежа
отмечаем
следующие
случаи:
1)
CQ > МК, т.
е.
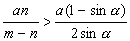 , что по
упрощении
дает
, что по
упрощении
дает
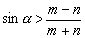 . Если это
условие
выполнено, то
задача имеет
максимум два
решения (треугольник
АВС и
ему
симметричный
относительно
ВС).
. Если это
условие
выполнено, то
задача имеет
максимум два
решения (треугольник
АВС и
ему
симметричный
относительно
ВС).
2)
CQ = МК,
иначе говоря,
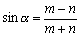 ; задача имеет
максимум четыре
решения (треугольники
АВС, ВСК
и им
симметричные
относительно
BQ).
; задача имеет
максимум четыре
решения (треугольники
АВС, ВСК
и им
симметричные
относительно
BQ).
3)
CQ < МК, т.
е.
 ; задача имеет
максимум шесть
решений (треугольники
АВС, А1ВС,
А2ВС и им
симметричные
относительно
BQ).
; задача имеет
максимум шесть
решений (треугольники
АВС, А1ВС,
А2ВС и им
симметричные
относительно
BQ).
Уточним
случаи
минимума
решений.
В первом
случае
решение
будет одно,
если
треугольник АВС
равнобедренный.
Это случится,
если АВ
равно ВС (случай АС=ВС
невозможен,
так как m
>
n;
аналогично
невозможно,
чтобы
треугольник АВС
был
равносторонним,
так как m
Ή
n).
Пусть АВ=ВС=а
(рис. 44 б). Тогда ВР
=
-а
cos2a.
По условию
 , откуда
, откуда
 , или
, или
 .
.
Итак, если
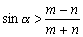 и
одновременно
и
одновременно
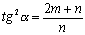 , то задача
имеет одно
решение.
, то задача
имеет одно
решение.
Покажем, что
во втором
случае
задача имеет
три решения
при
следующих
условиях:
а)
Треугольник ВСК
будет
равнобедренным
только при
условии, если a
= 30°,
т. е.
 ; в этом
случае m=3n.
При этих
условиях
треугольник АВС
неравнобедренный,
так как
система
равенств
; в этом
случае m=3n.
При этих
условиях
треугольник АВС
неравнобедренный,
так как
система
равенств

при
a
=
30° и
m=3n
противоречива.
б) Если
 и
и
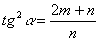 , иначе говоря,
когда
, иначе говоря,
когда
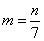 , то в этом
случае
только один
треугольник АВС
равнобедренный.
Задача не
может иметь
менее трех
решений, так
как
треугольник АВС и ВСК
вместе не
могут
оказаться
равнобедренными
(тогда
требовалось
бы
одновременное
выполнение
двух
равенств: m=3n и 7m=n),
они не могут
также и
совпасть при
построении.
, то в этом
случае
только один
треугольник АВС
равнобедренный.
Задача не
может иметь
менее трех
решений, так
как
треугольник АВС и ВСК
вместе не
могут
оказаться
равнобедренными
(тогда
требовалось
бы
одновременное
выполнение
двух
равенств: m=3n и 7m=n),
они не могут
также и
совпасть при
построении.
В третьем
случае
минимальное
число
решений
пять, так как
только какой-нибудь
один из трех
треугольников
может быть
равнобедренным.
Аналитическое
выражение
условий
случая пяти
решений
получить
нетрудно.
II.
(90°
<
a
< 180°,
m >
n)
отличается
от первого
тем, что QA²
не имеет
общих точек с
дугой
сегмента.
Задача может
иметь
максимум два
решения.
Выше
сказано, что
от выбора
варианта
анализа
зависит
сложность
исследования.
Однако
окончательные
результаты
исследования
от способа
решения не
зависят. Это
утверждение
не нуждается
в особом
доказательстве,
оно следует
из
возможности
выяснить
условия
существования
фигуры чисто
аналитическим
путем в
достаточно
общем виде.
Сделаем
несколько
замечаний об
исследовании
в задачах,
решаемых
алгебраическим
методом.
Как
уже отмечено
ранее,
алгебраический
анализ
включает в
себя и
некоторые
вопросы
исследования.
Этап
исследования
как бы
раздваивается,
одна часть
его
проникает в
этап анализа.
Мы будем
считать, что в
задачах,
решаемых
алгебраическим
методом,
исследование
состоит из
двух частей:
одной,
осуществляемой
в анализе, и
другой,
осуществляемой
в этапе
исследования.
Здесь надо
иметь в виду
следующее.
Из
рассмотренных
в §5 примеров
видно, что, во-первых,
с точки
зрения
алгебраической
мы
ограничивались
действительными
корнями
уравнения (исходя
из
геометрического
смысла
неизвестного).
Это
требование
принадлежности
корней полю
действительных
чисел было
необходимым
условием
наличия
геометрического
решения
задачи. Во-вторых,
мы находили
еще
достаточные
условия того,
что
найденный
корень
являлся
решением
задачи. Не все
действительные
корни
являлись
обязательно
решением
задачи;
например, в
некоторых
случаях
отбрасывался
отрицательный
корень.
Возможно, что
условия
наличия
действительного
корня
потребуется
сузить (или,
наоборот,
расширить),
для того
чтобы они
стали
достаточными.
В-третьих, при
рассмотрении
примеров
почти
совершенно
оставался в
стороне
вопрос о
геометрической
сути
найденных
необходимых
и
достаточных
условий
годности
того или
иного корня.
Наконец, в-четвертых,
совсем не
решался
вопрос о
числе
решений
задачи. Дело в
том, что, как
указывает П.
Некрасов, «при
высчитывании
числа
решений
задачи нужно
иметь в виду,
что число
годных
решений
уравнений
задачи не
всегда
совпадает с
числом
решений
самой задачи».
Подсчет
числа
решений
может
потребовать
дополнительного
графического
исследования
найденных
корней.
Мы видим,
что
сформулированные
выше моменты
исследования
для случая
алгебраического
анализа
необходимо
дополнить
такими
моментами:
а)
алгебраическое
исследование
существования
действительных
корней.
б)
исследование
пригодности
действительных
корней
уравнения,
исходя из
геометрического
смысла
задачи.
в) уточнение
и
геометрическое
истолкование
условий
наличия
решений.
г) подсчет
числа
решений.
Рассмотрим
несколько
примеров,
чтобы
выяснить, как
осуществляются
эти четыре
момента.
В анализе
задачи 15: построить
прямоугольный
треугольник
по s1=c+b
и s2=c+a (§4)
мы уже
осуществили
моменты а, б и
в. Из
построения
следует, что
треугольник АВС
можно еще
подвергнуть
преобразованию
симметрии
относительно
АВ, и
задача,
вообще
говоря, имеет два
решения. Если s1=s2=s
задача
имеет одно
решение (равнобедренный
треугольник).
Исследование,
а вместе с ним
и решение
этой задачи
можно
считать
законченным.
Заметим, что
здесь при
одном годном
корне
уравнения мы
имеем
максимум два
решения.
Проведем
исследование
задачи 17: через
две данные
точки А и В
построить
окружность,
касательную
к данной
прямой PQ.
В анализе
задачи (§4)
вместе с
решением
вопроса о том,
что как
положительный,
так и
отрицательный
корни
приводят к
решению, дан
ответ
и на вопрос о
максимальном
числе
решений.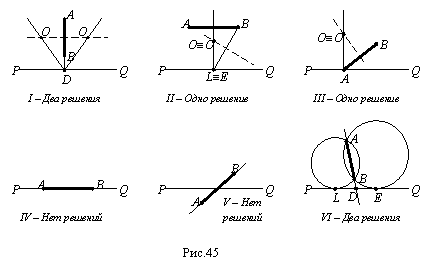
Однако
исследование
задачи еще не
закончено. Мы
имеем здесь
пример, когда
в задаче,
решаемой
алгебраическим
методом,
необходимо
провести
обычное для
задач
положения
геометрическое
исследование.
В анализе,
построении и
доказательстве
принималось,
что прямая АВ
пересекает
прямую PQ.
Теперь надо
рассмотреть
различные
случаи
взаимного
положения
прямых АВ
и PQ.
Эти случаи
даны на
рисунке 45.
В этом
примере
также видно,
что число
годных
корней
уравнений не
всегда
совпадает с
числом
решений
задачи.
В некоторых
случаях
чисто
алгебраическое
решение
задачи на
построение
сильно
упрощается,
если в
известный
момент
алгебраический
анализ
сочетать с
геометрическим
анализом.
Приведем
пример.
Задача
22.
Построить
прямоугольный
треугольник
с периметром 2р,
равновеликий
данному
квадрату,
сторона
которого к.
Проведем
сначала
алгебраическое
решение,
выполнив
исследование
полностью,
включая и его
часть,
содержащуюся
в анализе.
Если катеты
искомого
треугольника
х и у,
то:
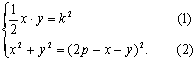
Решая эту
систему,
получим
сумму
катетов:
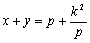 .
(3)
.
(3)
Теперь
имеем
произведение
и сумму
искомых
отрезков и
при помощи
теоремы
Виета
получим
уравнение:
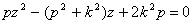 .
.
Корни этого
уравнения:
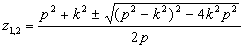 , где z1
и z2
катеты
искомого
треугольника.
, где z1
и z2
катеты
искомого
треугольника.
Исследование.
а) Так как
имеют смысл
лишь
вещественные
значения
корней, то (р2
-
к2)2 ³ 4к2р2,
или
р2-к2 ³ 2кр
(4)
б) Исследуем,
оба ли
значения z
надо
учитывать.
Так как
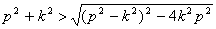 , то следует
учесть оба
значения
корня,
поэтому
возможны две
комбинации:
, то следует
учесть оба
значения
корня,
поэтому
возможны две
комбинации:
z1
= x, z2
= y и z1 = y, z2
= x.
в) Выясним
геометрический
смысл
условия (4)
существования
решения.
Прибавив к
обеим частям
неравенства
(4) по 2к2,
получим:
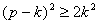 , или
, или
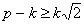 , т. е.
, т. е.
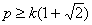 .
.
Условие
существования
решения
теперь
выражено при
помощи
данных
отрезков.
г) Выясним
число
решений
задачи.
Если
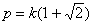 , то z1=z2=x=y, и
задача имеет
одно решение
равнобедренный
треугольник
с катетами
, то z1=z2=x=y, и
задача имеет
одно решение
равнобедренный
треугольник
с катетами
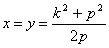 .
.
Если
 , то две
указанные в
пункте (б)
комбинации
значений z
дают два
решения (х
Ή
у,
треугольники
неравнобедренные).
, то две
указанные в
пункте (б)
комбинации
значений z
дают два
решения (х
Ή
у,
треугольники
неравнобедренные).
Однако
решение
можно
провести и по-другому.
Так как с
=
2р -
(х+у), то,
учитывая
равенство (3),
получим:
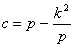 .
(5)
.
(5)
Задача
свелась к
построению
прямоугольного
треугольника
по сумме
катетов и
гипотенузе.
Для решения
этой
последней
задачи лучше
воспользоваться
геометрическим
анализом.
Выясняем,
каким
образом в
чертеж-набросок
включить
отрезок х+у
(рис. 46 а). После
этого
искомая
точка В
отыскивается
по таким ее
свойствам: В
принадлежит
лучу DB,
наклоненному
к AD
под углом 45°,
и В Μ
(А, с).
Очевидно,
что и
исследование
в этом случае
будет иметь
геометрический
характер. В
исследовании
выясняем
следующие
пять случаев (рис.
46 б):
1)
с<АК
нет решений;
2)
с=АК
одно решение
(равнобедренный
треугольник АСК);
3)
АК<
с <
а + b
два решения
(треугольники
АВС1
и АВ2С2);
4)
и
5) с ³
a
+ b нет
решения.
Задача не
имеет
решения, если с<АК.
Так как
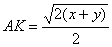 , то, учитывая
равенства (3) и (5),
получим
следующее
условие
отсутствия
решений:
, то, учитывая
равенства (3) и (5),
получим
следующее
условие
отсутствия
решений:
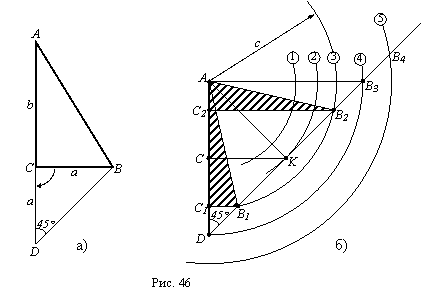 Eсли
Eсли
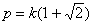 , то задача
имеет одно
решение
прямоугольный
равнобедренный
треугольник АСК
(рис. 46 б). Задача
имеет два
решения, если
, то задача
имеет одно
решение
прямоугольный
равнобедренный
треугольник АСК
(рис. 46 б). Задача
имеет два
решения, если
 .
.
Замечаем,
что чисто
алгебраическое
решение
более сложно;
это будет еще
очевиднее,
если
выполнить
построение
на основании
алгебраического
анализа:
построение
корней z1 и z2 много
сложнее, чем
построение
отрезков
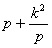 и
и
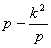 .
.
ΠΡΠΏΠΎΠ»ΡΠ·ΡΡΡΡΡ ΡΠ΅Ρ
Π½ΠΎΠ»ΠΎΠ³ΠΈΠΈ
uCoz Нами
выбрана в
качестве
руководящей
в анализе
идея
отыскания
так
называемых
искомых
элементов (точек)
фигуры по их
свойствам и
отнесение
элемента
двум
геометрическим
образам.
Отсюда
следует
самое общее
выражение
идеи
исследования:
выяснение
всех
характерных,
отвечающих
задаче
случаев
взаимного
расположения
двух
геометрических
образов, к
которым
принадлежит
искомый
элемент
Нами
выбрана в
качестве
руководящей
в анализе
идея
отыскания
так
называемых
искомых
элементов (точек)
фигуры по их
свойствам и
отнесение
элемента
двум
геометрическим
образам.
Отсюда
следует
самое общее
выражение
идеи
исследования:
выяснение
всех
характерных,
отвечающих
задаче
случаев
взаимного
расположения
двух
геометрических
образов, к
которым
принадлежит
искомый
элемент  Границы
изменения
параметра
выявляются в
ходе
исследования,
когда
графически,
путем
испытаний, мы
стараемся
получить все
новые
характерные
случаи
взаимного
расположения
интересующих
нас
геометрических
мест.
Некоторые
элементы
чертежа для
исследования
помогают
быстрее
установить
эти случаи. В
рассматриваемом
примере
такими
элементами
будут
отрезки ВС=а
и КС=а
Границы
изменения
параметра
выявляются в
ходе
исследования,
когда
графически,
путем
испытаний, мы
стараемся
получить все
новые
характерные
случаи
взаимного
расположения
интересующих
нас
геометрических
мест.
Некоторые
элементы
чертежа для
исследования
помогают
быстрее
установить
эти случаи. В
рассматриваемом
примере
такими
элементами
будут
отрезки ВС=а
и КС=а 1)
задачи
метрические,
в которых
требуется
построить
фигуру,
имеющую
заданные
размеры и
форму, но
произвольно
расположенную
на плоскости;
в этих
задачах
фигура
отыскивается,
как говорят, «с
точностью до
положения на
плоскости»;
1)
задачи
метрические,
в которых
требуется
построить
фигуру,
имеющую
заданные
размеры и
форму, но
произвольно
расположенную
на плоскости;
в этих
задачах
фигура
отыскивается,
как говорят, «с
точностью до
положения на
плоскости»; Пользуясь
результатами
анализа и
построения,
воспроизводим
часть
построения
на отдельном
чертеже,
стремясь
сохранить
конфигурацию,
имевшую
место в
соответствующей
части
построения (масштаб
не
соблюдается).
Например, в
рассматриваемом
случае
изображаем
основание ВС,
острый угол А
Пользуясь
результатами
анализа и
построения,
воспроизводим
часть
построения
на отдельном
чертеже,
стремясь
сохранить
конфигурацию,
имевшую
место в
соответствующей
части
построения (масштаб
не
соблюдается).
Например, в
рассматриваемом
случае
изображаем
основание ВС,
острый угол А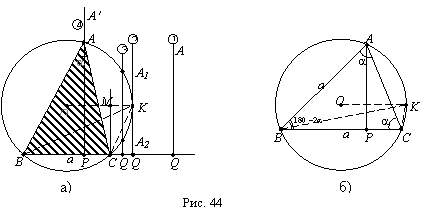 Исследование. Изображаем
на отдельном
чертеже ГМТ,
из которых
отрезок а
виден под
углом
Исследование. Изображаем
на отдельном
чертеже ГМТ,
из которых
отрезок а
виден под
углом 

 Eсли
Eсли