<<Предыдущая страница

В. А. Ассонова, Н. В. Ассонова

Раздел 1. Задачи на построение

з 1.5. Цель, принцип и основные моменты анализа в решении задач на построение

Затруднения, с которыми многие сталкиваются при проведении анализа в задаче на построение, объясняются отсутствием ясной общей идеи, при помощи которой можно построить всю логическую цепь рассуждений.

Из всего сказанного в предыдущих параграфах со всей определенностью следует, что такой идеей анализа можно считать идею метода геометрических мест.

Цель анализа Ц отыскание пути решения задачи и выяснение плана построения.

Основной принцип анализа следует из его идеи и заключается в установлении и отыскании искомых элементов фигуры по геометрическим свойствам этих элементов.

Приняв принцип анализа Ц отыскание искомых элементов по их геометрическим свойствам, мы имеем в виду отыскание всех без исключения элементов, обладающих определенными, следующими из условия задачи свойствами. Тем самым выполняется так называемый лпринцип полноты╗ анализа, гласящий, что правильно проведенный анализ гарантирует отыскание всех решений задачи, если она имеет несколько решений.

Для достижения цели анализа необходимо выполнить принятый принцип путем осуществления следующих основных моментов анализа.

1. Предположение, что задача решена. Выполнение чертежа-наброска. Сделаем формальное предположение, что задача решена, и выполним чертеж-набросок фигуры (аккуратно от руки, возможно в более общем виде). Чертеж-набросок закончен, если выполнены два требования: в него включены все данные элементы; данные элементы особо помечены (например, при помощи цветных мелков).

В чертеже-наброске не требуется соблюдение масштаба.

2. Указание определяющих элементов требуемой фигуры и установление среди них искомых. Рассматривая чертеж-набросок, устанавливаем определяющие элементы фигуры. Известные определяющие элементы отмечаем на чертеже-наброске условным способом (например, обводя их кружками). Неизвестные определяющие элементы суть искомые. Особое внимание уделяется установлению этих искомых элементов. Обычно такими элементами будут точки Ц вершины многоугольников, центр искомой окружности и т. д.

Выбор тех или иных из определяющих элементов в качестве известных или искомых не всегда однозначен; иногда возможно несколько как приемлемых, так и неприемлемых вариантов.

3. Установление геометрических свойств искомых элементов.

Указав искомые элементы, утверждаем, что для отыскания искомого надо знать геометрические свойства этого искомого.

Свойства искомых элементов устанавливаются при помощи чертежа-наброска, причем основное внимание уделяется обнаружению связи искомых точек с известными элементами.

Связь искомых элементов с данными, зависимость между ними и определяют геометрические свойства искомых элементов.

Часто для установления свойств одного из искомых элементов необходимо использовать новые неизвестные элементы, которые, в свою очередь, играют роль искомых (см., например, задачу 18).

Как уже указано, если при изучении чертежа-наброска свойства искомых элементов не выявляются, необходимо применить геометрические преобразования.

4. Отнесение искомых элементов к тем или иным геометрическим образам. Установив последовательно два свойства искомой точки, мы отнесем ее к двум геометрическим местам, образы которых обычно известны. Так как искомая точка принадлежит одновременно и тому и другому геометрическому месту, то делается вывод, что если эта точка существует, то является точкой пересечения известных геометрических образов. Выражение лесли эта точка существует╗ уже выдвигает проблему исследования.

5. Составление плана построения. Последним моментом анализа является подведение его итогов в виде плана построения. При осуществлении вышеизложенного принципа план построения всегда очевиден, поэтому если анализ в краткой форме зафиксирован, то план построения не записывается. Основные пункты плана формулируются на основе тех выводов, которыми всякий раз заключались рассуждения по каждому из искомых элементов.

Примечание. Алгебраический анализ проводится в общем исходя из основного принципа, но отличается некоторым своеобразием, так как включает в себя элемент исследования.

Применение только что изложенных моментов уже осуществлено в ряде задач, рассмотренных выше. Приведем несколько новых примеров.

Задача 18. Построить треугольник по b, m_c, R (рис. 34).

Цель этого примера Ц показать, как ведется анализ в том случае, когда его основной принцип осуществляется применением метода геометрических мест.

Анализ. Предположим, что задача решена и треугольник АВС Ц искомый. Выполним чертеж-набросок; в него включим все данные в задаче элементы. Отметим эти данные на чертеже.

Установим по чертежу-наброску определяющие элементы фигуры. Это будут вершины треугольника А, В, С. Среди них известны А, С. Искомый элемент Ц вершина В.

Чтобы найти искомое, надо знать его свойства. Геометрическим свойством точки В, во-первых, является ее принадлежность данной окружности (О, R): В╠(О, R).

Второе свойство точки В не очевидно. Изучаем чертеж-набросок; пока нами не учтена в рассуждениях медиана m_c. Замечаем, что искомая вершина В принадлежит прямой AD. Но положение прямой AD не определено. Оно определится, если будет найдена точка D. Появляется новый искомый элемент Ц точка D.

Первое свойство точки D очевидно: она удалена от данной точки С на данное расстояние m_c: D принадлежит окружности (С, m_c). Второе свойство точки D не очевидно. Известно лишь, что D Ц середина АВ. Что означает это свойство, пока не ясно (если не изучено соответствующее ГМТ). АВ Ц хорда окружности, проходящая через точку А, точка D Ц середина этой хорды. Построив отрезок OD, видим, что ╨ADO Ц прямой, т. е. из точки D отрезок АО виден под прямым углом. Поэтому D принадлежит окружности (О₁, ).

Вывод 1-й. Точка D, если она существует, является точкой пересечения окружностей (С, m_c) и (О₁, ).

Вывод 2-й. Если точка D существует, то прямая AD определена, и тогда точка В найдется как точка пересечения окружности (O, R) и прямой AD.

Нам осталось сформулировать план построения. Он прост.

а) Вписать, если возможно, хорду АС=b в окружность (О, R);

б) Построить окружность (О₁, );

в) Построить окружность (С, m_c) и отыскать точку D пересечения окружностей (О₁, ) и (С, m_c);

г) Если D существует, то построить AD до пересечения с (О, R) в точке В, наконец, построить ВС и АВ.

Задача 19. В данный квадрат вписать равносторонний треугольник, одна из вершин которого (на стороне квадрата) дана.

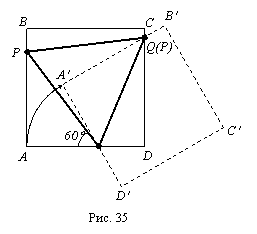
Анализ. Пусть треугольник PQR Ц искомый (рис. 35), R Ц его известная вершина. Достаточно найти еще одну вершину треугольника, пусть Q. Точка Q Ц искомая. Q╠CD. Для выяснения второго свойства точки Q выполним преобразование поворота всей изображенной фигуры вокруг центра R на угол 60░. Тогда точка P преобразуется в Q, а квадрат ABCD преобразуется в квадрат AвBвCвDв. При этом положение прямой АвВв известно. Отсюда Ц второе свойство точки Q (собственно, точки Р, но здесь точка Р совпала с точкой Q): Q╠АвВв.

Вывод. Точка Q, если она существует, является точкой пересечения прямых АвВв и CD.

Таким образом, в данной задаче идея анализа реализована при помощи метода поворота.

Задача 20. К двум данным окружностям w(О, R) и w₁(О₁, r) построить общую внешнюю касательную

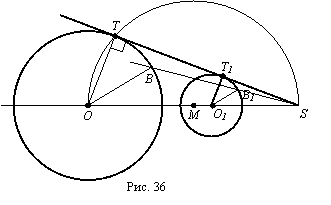Анализ. Предположим, что задача решена. Для отыскания точки Т (рис. 36) отметим одно ее очевидное свойство: Т принадлежит окружности (О, R).

Далее замечаем, что ╨ОТТ₁=90░. Если продолжить ТТ₁ до пересечения с ОО₁ в точке S, то очевидно, что Т принадлежит окружности (М, ). Теперь точка S Ц искомая.

Существенным свойством точки S является то, что она есть центр гомотетии (прямой) окружностей w и w₁. Поэтому (рис. 36) точка S есть точка пересечения прямых ОО₁ и ВВ₁, где ОВ Ц произвольный радиус окружности w, О₁В₁||ОВ. Окончательно: Т есть точка пересечения двух окружностей: (О, R) и (М, ).

 Для реализации идеи анализа в этой задаче применен метод гомотетии.

Рассмотрим еще один вариант решения этой задачи.

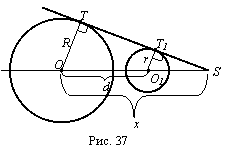
Пусть ТТ₁ Ц искомая касательная (рис. 37). Продолжим ее до пересечения с ОО₁. Точка S Ц искомая. S╠ОО₁, второе ее свойство: S принадлежит окружности (О, OS).

Обозначим неизвестный отрезок OS=x. Треугольники OTS и O₁T₁S подобны, отсюда:

,

т. е. х Ц четвертый пропорциональный отрезок трем известным отрезкам: R, d и R-r.

В данном варианте решения идея анализа реализована при помощи алгебраического метода.

Следующая страница>>