<<Предыдущая страница

В. А. Ассонова, Н. В. Ассонова

Раздел 1. Задачи на построение

� 1.4. Алгебраический метод

Между длинами отрезков, входящих в какую-либо фигуру, можно установить некоторые числовые зависимости. Те из зависимостей, которые не зависят от выбора единицы длины, называются метрическими соотношениями. Каждое из таких соотношений можно представить в виде:

x=f(a, b, c, �, k, e), где a, b, c, �, k, e � длины некоторых отрезков, х � длина отрезка. Функция f(a, b, c, �, k, e) определена в некоторой области положительных значений своих аргументов и принимает в этой области, вообще говоря, только положительные значения. Примеры таких соотношений приведены ниже.

Условие, при котором соотношение x=f(a, b, c, �, k, e) определяет, независимо от выбора единицы измерения, один и тот же отрезок, состоит в том, чтобы f являлась однородной функцией первой степени от своих аргументов (справедливо и обратное утверждение).

Так как в этом случае соотношение x=f(a, b, c, �, k, e) не зависит от выбора единицы длины, то его естественно назвать соотношением между самими отрезками.

Применение только что сказанного к задачам на построение заключается в следующем. Любое требование о построении фигуры F, после того как искомые элементы ее указаны, можно свести далее к нахождению некоторых соотношений, выражающих искомые элементы через данные. При этом используются метрические соотношения, известные для искомой фигуры. Эти соотношения обычно приводят к уравнениям или системам уравнений. Решая уравнение или систему уравнений методами алгебры, получают новые зависимости в виде формул, выражающих неизвестные отрезки через данные элементы.

Если х � отрезок, то f � обязательно однородная функция первой степени. Далее остается выполнить построение этого отрезка, благодаря чему искомый элемент фигуры будет найден.

Мы считаем известным построение при помощи циркуля и линейки следующих выражений:

x=a+b; x=a-b, где a>b;

x=n�a; , где n � целое, неравное нулю число;

 - отрезок, четвертый пропорциональный трем данным отрезкам;

 - отрезок, средний пропорциональный между двумя данными отрезками;

 (a>b).

Полагаем известными также все способы построения корней квадратных уравнений (в отрезках).

Приведенные основные выражения отрезка х, который можно построить циркулем и линейкой, позволяют выполнить построения более сложных выражений.

Приложение алгебры к решению вопроса о геометрических свойствах искомых элементов путем установления определенных соотношений между некоторыми неизвестными элементами и элементами данными и является характерным признаком так называемого алгебраического метода решения задач на построение.

Ценность алгебраического метода состоит прежде всего в том, что методами алгебры (именно высшей алгебры) удалось окончательно определить класс задач, разрешимых при помощи циркуля и линейки. Было доказано, что этими средствами можно построить все те и только те отрезки, которые являются корнями алгебраического уравнения, имеющего своими коэффициентами рациональные функции (с рациональными числовыми коэффициентами) от данных отрезков и разрешимого в квадратных радикалах.

Рассмотрим применение алгебраического метода в задачах на построение, разрешимых циркулем и линейкой.Предположив задачу решенной, стараемся установить геометрические свойства искомых элементов. Если это трудно сделать геометрическими средствами, прибегаем к алгебраическому методу. Конкретный пример поясняет суть алгебраического анализа.

Задача 15. Построить прямоугольный треугольник по сумме s₁ гипотенузы с одним катетом и сумме s₂ гипотенузы с другим катетом.

Анализ. Сделаем чертеж-набросок, введя в него все данные элементы

(рис. 31).

Вспомогательный треугольник А₁В₁С можно построить, но как перейти от него к искомому, из чертежа не усматриваем.

Геометрическое решение этой задачи далеко не очевидно (см. зада-

чу 14). Продолжим анализ средствами алгебры.

Ясно, что если бы отрезок ВВ₁ (равный АА₁) был известен, то мы смогли бы выполнить переход от треугольника А₁В₁С к искомому, так как свойства точек В и А были бы известны. Исходя из этого соображения, обозначаем отрезок ВВ₁ при помощи неизвестного х (�неизвестный отрезок�). Так как ВВ₁=ВА=х, то СВ=s₁-х, СА=s₂-х, и по теореме Пифагора имеем:

.

Откуда после упрощения имеем уравнение:

.

Общее выражение корней этого уравнения таково:

,

х � отрезок, выраженный однородной функцией первой степени от отрезков s₁ и s₂. В выражение функции входит лишь квадратный радикал, значит, построение х при помощи циркуля и линейки возможно. Встает вопрос о выборе соответствующего знака перед радикалом.

Здесь мы начинаем ставить вопросы, которым, вообще говоря, место в исследовании. В этом особенность алгебраического анализа.

Чем же мотивируется выбор знака?

По условиям задачи  x < s₁, x < s₂.

Этим условиям не удовлетворяет выбор знака (+) перед корнем, так как тогда получим: х > s₁ и х > s₂.

Выберем поэтому знак (-):

.

Проверим, выполняется ли условие задачи. Необходимо, чтобы система:

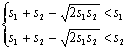                             (1)

была непротиворечивой.

Если s₁=s₂=s, то имеет место неравенство:

, или ,

что справедливо, так как рассуждения обратимы, то, следовательно, условие задачи выполняется.

Если s₁�s₂ и, например, s₁>s₂, то из системы (1) получаем неравенство:

, или ;

возводя обе части неравенства в квадрат, имеем:

, или .

Таким образом, выбранный корень удовлетворяет условию задачи и в том случае, когда s₁>s₂, если .

Вывод. Задача имеет решение, если s₁=s₂ и s₁�s₂, но половина большего отрезка менее второго, меньшего. В других случаях задача не имеет решения.

Обратим внимание, что по окончании исследования мы можем судить лишь о наличии или отсутствии решений, сравнивая заданные отрезки, т. е. результаты исследования истолковываются геометрически, исходя из данных элементов.

Рассмотренная задача является типичным примером того, когда геометрическое решение достаточно сложное, а алгебраический анализ быстро приводит к цели.

Приведем пример задачи, когда при выборе знака перед радикалом, исходя из условий задачи, необходимо брать оба значения корня.

Задача 16. Построить прямоугольник, равновеликий данному квадрату ABCD с площадью q² (q � данный отрезок), если периметр прямоугольника 2р.

Анализ. Очевидно, что, определив длины сторон х и у прямоугольника, построить искомую фигуру просто. Имеем систему:

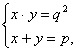                               (1)

решая которую при помощи теоремы Виета, получим:

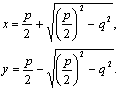
Так как и х>0 и у>0, то оба значения дают решение, если .

Система (1) может быть решена и по-другому. Перепишем ее так:

Вычтем из второго уравнения первое:

.

Если р � гипотенуза, 2q � катет некоторого прямоугольного треугольника, то второй его катет m=x-y.

Отрезок m может быть найден построением. Теперь, зная сумму и разность сторон прямоугольника, можно найти его стороны.

Этот вариант, несколько искусственный с алгебраической точки зрения, усложняет построение искомой фигуры.

Приведем, наконец, случай, когда при исследовании формулы для неизвестного нельзя отбрасывать и отрицательное значение его.

Задача 17. Через две данные точки А и В построить окружность, касательную к данной прямой PQ.

Анализ. Искомая точка � центр О окружности (рис. 32).

Первое свойство: О принадлежит серединному перпендикуляру к отрезку АВ; второе свойство: О�ЕО, ЕО^PQ, но положение точки Е на прямой PQ неизвестно. Теперь точка Е � искомая: Е�PQ.

Построим АВ до пересечения с PQ в точке D. Очевидно, второе свойство точки Е: Е принадлежит окружности (D, DE). Но отрезок DE неизвестен.

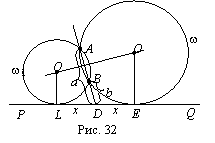Пусть DE=x. Если AD=a, BD=b, то .

Положительное значение х требует построения этого отрезка на PQ вправо от D. Отрицательное значение х требует отложить х на PQ влево от точки D.

Мы видим, что здесь формула исследована в отношении пригодности отрицательного значения х. Собственно говоря, это исследование надо было бы выполнить после построения, так как оно дает ответ на вопрос о числе решений.

Приведем еще один вариант анализа этой задачи. Он основывается на той же теореме о касательной и секущей (построенных из одной точки), но при этом выполняются некоторые дополнительные построения.

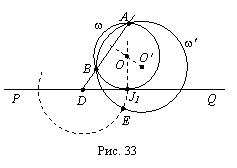
Точка О � искомая (рис. 33). О принадлежит серединному перпендикуляру к отрезку АВ и О�OY₁, OY₁^MQ.

Теперь точка Y₁ � искомая. Кроме того, что Y₁�MQ, пока ничего неизвестно.

Построим какую-нибудь окружность w�, проходящую через точки А и В, затем построим касательную DE к этой окружности. Имеем:

AD�BD=DY₁²=DE²,

т. е. DY₁=DE.

Следовательно, Y₁ принадлежит окружности (D, DE). Очевидно, что точка Y₂ приводит ко второму решению задачи.

Приведенные примеры показывают, что применение алгебры к решению геометрических задач на построение вызывает некоторую ломку схемы решения задачи. Исследование приходится частично проводить в ходе анализа. Исследование касается алгебраической стороны дела: например, позволяет отобрать решения уравнения, установить область существования функции x=f(a,b,c,�,k) и т. д.

Следующая страница>>