<<Предыдущая страница

В. А. Ассонова, Н. В. Ассонова

Раздел 1. Задачи на построение

 з 1.3. Геометрические преобразования и их применение для  решения задач на построение

Мы рассмотрим приложение к решению задач на построение некоторых так называемых точечных преобразований плоскости в себя. Каждое такое геометрическое преобразование понимают как операцию, позволяющую по известному закону находить (однозначно) для данного геометрического элемента (точки) плоскости элемент (точку) той же плоскости.

Точечные преобразования являются в сущности геометрической реализацией понятия функции.

В общем случае необходимость применения геометрических преобразований для решения задачи на построение вытекает из следующего: когда свойства искомых элементов фигуры, которую требуется построить, невозможно обнаружить при изучении первоначального чертежа-наброска, то прибегают к геометрическим преобразованиям либо всей изображенной на чертеже-наброске фигуры, либо ее элементов. При этом либо сама фигура приобретает новое качество, либо появляется новая фигура (лвспомогательная╗), изучение которой позволяет вскрыть свойства искомых элементов фигуры.

Реализация этой идеи в анализе и будет характерной особенностью применения соответствующего лметода преобразования╗ для решения задач на построение.

1. Симметрия относительно прямой. Метод симметрии

Пусть дана точка А плоскости. Построим произвольную прямую s, не содержащую точку А. Построим перпендикуляр АА₀^s  (где А₀ ╠ s) и отрезок А₀Ав этого перпендикуляра так, что АА₀=А₀Ав. Назовем Ав образом точки А при симметрии относительно прямой s. Прямую s назовем осью симметрии. Установим взаимно однозначное соответствие между А и Ав. Тогда и А есть образ точки Ав, т. е. А и Ав взаимно симметричные точки. Таким образом, для каждой точки М плоскости можно найти соответственную ей точку, если задать ось симметрии s.

Операция установления соответствия между точками плоскости при помощи симметрии относительно прямой называется преобразованием симметрии относительно прямой, или просто осевой симметрией.

Достаточно задать ось симметрии, чтобы определить симметрию как преобразование плоскости в себя. При этом точки оси симметрии сами себе соответствуют.

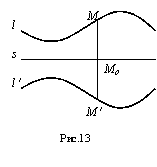
Пусть на плоскости дан некоторый геометрический образ, например кривая l, и указана ось симметрии s. Тогда существует образ кривой l при симметрии относительно оси s, именно кривая lв (рис. 13). Кривую lв можно считать геометрическим местом образов точек кривой l.

Нетрудно установить, что образом прямой является прямая, образом отрезка является отрезок и что взаимно симметричные фигуры[1] F₁ и F₂ равны и противоположно ориентированы (зеркально равны), поэтому, вообще говоря, фигуру F₁ невозможно совместить со своим образом F₂ при помощи перемещения в плоскости.

Рассмотрим теперь применение симметрии относительно прямой при решении задач на построение.

В отдельных случаях для отыскания свойств искомых элементов целесообразно отразить фигуру F чертежа-наброска или некоторые ее части от надлежащим образом выбранной оси. При новом положении фигуры или ее частей иногда удается найти свойства искомых элементов.

Реализация этой идеи в анализе и будет характерным признаком применения метода осевой симметрии.

Проиллюстрируем примерами это общее положение.

Задача 5. Дан угол XOY, образованный лучами XO и OY, и точка А внутри этого угла. Найти на сторонах угла такие точки В и С, чтобы треугольник АВС имел наименьший периметр.

Анализ. Предположим, что задача  решена, треугольник АВ₁С₁ Ц искомый (рис. 14). Так как точка А дана, то одна вершина этого треугольника известна. Искомые точки Ц В₁ и С₁. Для отыскания их установим геометрические свойства этих точек.

Очевидно лишь одно свойство точки В₁: В₁╠OX. Второе свойство пока не усматривается.

Аналогично: С₁╠OY, и пока более ничего нельзя сказать о свойствах этой точки.

Попробуем для установления новых свойств точек В₁ и С₁ отразить точку А от прямых OX и OY; получим отражения точки А, соответственно Вв и Св. Построим отрезки ВвВ₁ и СвС₁. Очевидно, сумма ВвВ₁+В₁С₁+С₁Св равна периметру треугольника АВ₁С₁. Требуется, чтобы эта сумма была наименьшей, т. е. чтобы точки Вв, В₁, С₁ и Св принадлежали одной прямой ВвСв, положение которой известно.

Отсюда видно второе свойство точек В₁ и С₁: В₁╠ВвСв и С₁╠ВвСв.

Вывод. Искомые точки, если они существуют, суть точки пересечения лучей OX и OY с прямой ВвСв.

Приведем пример более сложной задачи.

Задача 6. Построить треугольник по а, h_a и разности углов В-С=l.

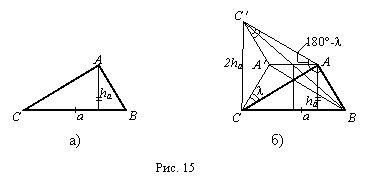
Анализ. Предположив, что треугольник АВС Ц искомый, замечаем (рис. 15а), что не все еще данные элементы включены в чертеж-набросок. Пока не закончен чертеж-набросок, анализ продолжать нельзя.

Для включения данного угла в чертеж-набросок отразим треугольник АВС от серединного перпендикуляра отрезка СВ. Тогда ╨АСАв =l (рис. 15б).

Вершины В и С треугольника известны. Искомая точка А.

Первое свойство точки А очевидно: она удалена от прямой ВС на расстояние h_a, поэтому А принадлежит ГМТ, удаленных на расстояние h_a от прямой ВС.

Второе свойство точки А далеко не очевидно. Для установления этого свойства отразим отрезок АС от прямой ААв.

Нетрудно видеть, что четырехугольник ВАвСвА Ц параллелограмм, в котором ╨АвСвА=l, поэтому ╨СвАВ=180░-l. Построим диагональ ВСв этого параллелограмма. Отрезок ВСв известен (точки В и Св известны). Этот отрезок виден под известным углом из точки А. Это и есть второе свойство искомой точки А. Поэтому А принадлежит ГМТ, из которых отрезок СвВ виден под углом 180░-l.

Вывод. Если точка А существует, то является точкой пересечения прямой ААв и дуги сегмента, построенного на отрезке СвВ и вмещающего угол 180░-l.

2. Параллельный перенос. Метод параллельного переноса

Пусть а₁ и а₂ Ц две параллельные прямые. Пусть Х Ц произвольная точка плоскости. Построим точку Хв, симметричную точке Х относительно прямой а₁, а затем построим точку Хвв, симметричную точке Хв относительно прямой а₂ (рис. 16). Преобразование, которое сопоставляет точке Х точку Хвв указанным образом, называется параллельным переносом.

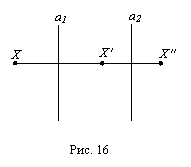
Можно показать, что это преобразование обладает следующим свойством: все отрезки, каждый из которых соединяет две соответственные точки, равны, параллельны и направлены в одну сторону (каждый из них равен удвоенному расстоянию между а₁ и а₂). Другими словами, фигура F₁ преобразуется в фигуру F₂ так, как будто все точки фигуры F₁ перенесены по прямым, перпендикулярным осям, в направлении от а₁ к а₂ на расстояние, равное удвоенному расстоянию между прямыми а₁ и а₂.

Преобразование переноса имеет большое применение при решении задач на построение; оно также служит цели раскрытия свойств искомых элементов. При этом чаще всего выполняется перенос некоторых известных элементов фигуры.

Рассмотрим следующий пример.

Задача 7. Даны окружность О, две ее точки А и В и прямая а, от которой окружность отсекает хорду CD. Требуется найти такую точку М окружности, чтобы отрезок PQ хорды CD, заключенный между хордами АМ и ВМ, был равен данному отрезку b.

Анализ. Пусть задача решена и точка М найдена (рис. 17).

Если будет отыскана одна из точек P или Q, то просто отыскать и точку М. Поэтому пусть, например, точка Q Ц искомая.

Пока очевидно лишь одно свойство этой точки: Q╠а.

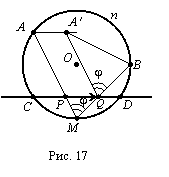
Второе свойство пока не усматривается. Для выяснения этого свойства выполним параллельный перенос, определяемый вектором . Тогда точка А преобразуется в Ав, точка P Ц в Q. Рассматривая образовавшуюся фигуру, видим такое свойство точки Q: отрезок АвВ из нее виден под углом j, который измеряется половиной известной дуги AnB. Поэтому, если точка Q существует, то она является точкой пересечения прямой а и дуги сегмента, построенного на отрезке АвВ и вмещающего угол j. Рассмотрим теперь следующую метрическую задачу.

Задача 8. Построить четырехугольник, если известны три его стороны и два внутренних острых угла, прилежащих к четвертой стороне.

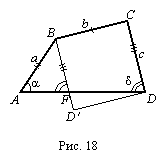Анализ. Примем за известные вершины четырехугольника точки А и В (рис. 18). Тогда вершины С и D Ц искомые. Достаточно найти одну из них.Установим, например, свойства точки D. Очевидно, что D╠AD. Второе свойство точки D пока неочевидно.Выполним (определяемый вектором ) параллельный перенос отрезка ВС. Тогда ломаная АВDв может быть построена, и становится очевидным второе свойство точки D: D принадлежит окружности (Dв, b).Дальнейший ход рассуждений ясен.Если в каждой из двух рассмотренных задач довести решение до конца, то мы будем иметь пример применения метода параллельного переноса в решении задач на построение.Во многих задачах на построение четырехугольников параллельный перенос быстрее приводит к цели, если заранее изучить основные свойства фигур, образующихся после определенного переноса некоторых элементов четырехугольника.

3. Центральная симметрия

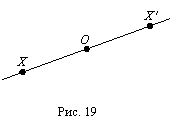
Пусть О Ц некоторая точка плоскости и Х Ц произвольная точка. Построим точку Хв по следующему правилу. Если точка Х совпадает с О, то Хв есть точка О. Если точка Х не совпадает с О, то точка Хв лежит на прямой ХО, причем точка О лежит между Х и Хв и расстояния ХО и ОХв равны (рис. 19). Построенная так точка Хв называется симметричной относительно точки О. Преобразование плоскости в себя, при котором каждой точке Х по указанному правилу сопоставляется точка Хв, называется преобразованием симметрии относительно точки О.

Во многих случаях для анализа в решении задачи на построение целесообразно применить центральную симметрию.

Рассмотрим две задачи.

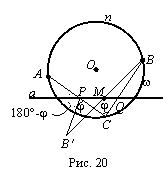Задача 9. Даны окружность w, две ее точки А и В, прямая а и ее точка М внутри окружности w. Требуется найти на окружности третью точку С, такую, чтобы прямые АС и ВС отсекали на прямой а отрезок, делящийся в точке М пополам.

Анализ. Предположив задачу решенной, видим (рис. 20), что построение решает точка Р╠а. Для установления еще одного свойства точки Р отразим В от точки М. Тогда В преобразуется в Вв и ВвР∥ВС, т. е. ╨ВвРС=╨ВСР=j. Отсюда очевидно, что отрезок АВв виден из точки Р под известным углом 180░-j, т. е. точка Р, если она существует, есть точка пересечения прямой а и ГМТ, из которых отрезок АВв виден под углом 180░-j.

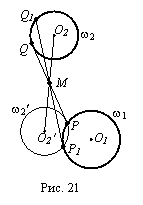Задача 10. Даны две окружности w₁ и w₂, точка М вне этих окружностей. Построить отрезок, концы которого принадлежат данным окружностям и который делится точкой М пополам.

Анализ. Достаточно найти одну из точек Р или Q искомого отрезка (рис. 21). Пусть Р Ц искомая точка. Отразим окружность w₂ от точки М. Тогда w₂ преобразуется в wв₂, а Q Ц в Р. Очевидно, что точки Р₁ и Q₁ дают второе решение. Отсюда вывод: если точка Р (или Р₁) существует, то она является точкой пересечения окружностей w₁ и wв₂.

Можно сказать, что обе эти задачи мы начали решать методом центральной симметрии.

4. Поворот

Пусть а₁ и а₂ Ц две различные прямые, пересекающиеся в точке О. Пусть Х Ц произвольная точка плоскости. Построим точку Хв, симметричную точке Х относительно прямой а₁, а затем построим точку Хвв, симметричную точке Хв относительно прямой а₂ (рис. 22.) Преобразование, которое сопоставляет точке Х точку Хвв указанным образом, называется поворотом относительно точки О.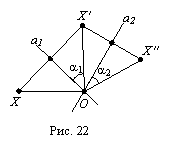Если прямые а₁ и а₂ перпендикулярны, то поворот сводится к симметрии относительно точки О. Если прямые а₁ и а₂ не перпендикулярны, то угол ХОХвв не зависит от точки Х и равен удвоенному острому углу, под которым пересекаются прямые а₁ и а₂. Этот угол называется углом поворота. Наметим доказательство этого утверждения.

Пусть точка Хв находится внутри острого угла, образованного прямыми а₁, а₂, и a₁, a₂ Ц части этого угла, на которые он разбивается полупрямой ОХв (рис. 22). Тогда по свойству симметрии относительно прямой угол ХОХв равен 2a₁, а угол ХвОХвв равен 2a₂. Соответственно угол ХОХвв равен 2a₁+2a₂=2(a₁+a₂). Читателю предлагается рассмотреть случай, когда точка Хв лежит внутри тупого угла, образуемого прямыми а₁ и а₂, а также случай, когда прямые а₁ и а₂ перпендикулярны.

Поворот прямой а на угол j вокруг центра О выполняется так.

Строится ОМ^а (М╠а). Затем в нужном направлении производится поворот отрезка ОМ на угол j в положение ОМв, после чего строится прямая ав^ОМв.

Отметим следующее очевидное свойство отражения фигур, обладающих осевой симметрией.

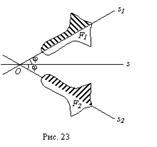
Преобразование симметрии относительно оси s, выполненное по отношению к фигуре, обладающей хотя бы одной осью симметрии, может быть заменено поворотом (в частном случае параллельным переносом).

Подвергнем фигуру F₁ (рис.23) преобразованию симметрии относительно прямой s. В результате получим фигуру F₂, противоположно ориентированную. Выполним для фигуры F₂ преобразование симметрии относительно оси s₂ (s₂ есть, очевидно, образ оси s₁). Тогда фигура F₂ преобразуется в себя и будет одинаково ориентирована с F₁, следовательно, фигуры F₁ и F₂ могут быть совмещены поворотом вокруг точки О пересечения оси симметрии фигуры и оси s. Если эти оси параллельны, то достаточно выполнить некоторый параллельный перенос.

Поворот на некоторый угол j г180░ имеет применение при решении задач на построение. При этом поворот выполняется либо по отношению ко всей фигуре чертежа-наброска, либо по отношению к отдельным элементам фигуры.

Рассмотрим примеры.

Задача 11. Даны точка О и прямые а и b, не проходящие через нее. Из точки О как из центра провести такую окружность, чтобы дуга ее, заключенная между данными прямыми, была видна из точки О под данным острым углом a.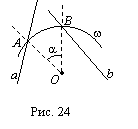Анализ. Допустим, что задача решена, w - искомая окружность, А и В Ц концы дуги, заключенной между данными прямыми, ╨АОВ = a (рис. 24). Если осуществить поворот прямой а около точки О на угол a, то точка А попадет в точку В. Следовательно, точка В может быть найдена как пересечение образа прямой а с прямой b. После этого легко строится искомая окружность.

Задача 12. Внутри данного треугольника АВС найти точку Р, сумма расстояний которой до вершин А, В и С была бы наименьшей.

Анализ. Пусть Р₁ Ц искомая точка. Для выяснения ее геометрических свойств повернем сначала треугольник АВР₁ на 60░ вокруг точки А

(рис. 25). Тогда АР₁+Р₁В+Р₁С=ВвРв+Р₁Рв+Р₁С.

Эта сумма будет наименьшей, если ВвС Ц прямая. Аналогичные рассуждения относительно треугольника ВР₁С (тогда В переходит в В▓) показывают, что АВ▓ - прямая.

Следующая страница>>