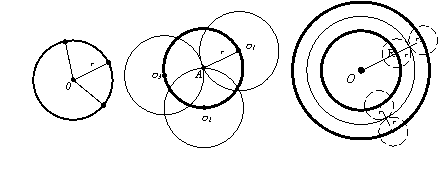
Следствие 2. ГМ центров окружностей радиуса r, касательных к окружности (O, R), R>r, есть совокупность двух окружностей, концентрических с данной: (O, R+r) и (O, R-r) (рис. 5).
В.
А. Ассонова, Н.
В. Ассонова
Раздел 1. Задачи
на
построение
¦ 1.2.
Геометрические
места точек,
обладающих
определенным
свойством.
Метод
геометрических
мест
(пересечения фигур)
Понятие
геометрического
места
является
одним из
важнейших в
геометрии.
Определение
геометрического
места точек
может быть
сформулировано
примерно так.
Геометрическим
местом точек,
обладающих
определенным
свойством,
называется
множество
всех точек,
которые
обладают
этим
свойством.
Это
определение
для
плоскости
означает, во-первых,
что заданием
свойств
точек мы как
бы выделяем (отличаем,
фиксируем)
некоторое
множество
точек
плоскости (это
множество
может быть
пустым,
конечным или
бесконечным,
может
составлять
некоторую
геометрическую
линию, а может
и не
составлять
таковой), во-вторых,
обратно,
изучая
свойства
точек
плоскости, мы
выделяем
некоторое
множество
этих точек по
их общим
свойствам (в
этом случае
множество
содержит
хотя бы один
элемент).
Приводим
далее
перечень
основных
геометрических
мест точек.
Этот
перечень не
претендует
на полноту.
1. ГМТ,
удаленных на
данное
расстояние r
от данной
точки О, есть
окружность
радиуса r
с центром в
точке О; (О, r)
(рис.3).
Следствие
1. ГМ
центров
окружностей
данного
радиуса r,
проходящих
через данную
точку А,
есть
окружность (А,
r)
(рис. 4).
Следствие
2. ГМ
центров
окружностей
радиуса r,
касательных
к окружности (O,
R), R>r,
есть
совокупность
двух
окружностей,
концентрических
с данной: (O,
R+r)
и (O,
R-r)
(рис. 5).
Рис.3
Рис.4
Рис.5
Замечание.
Можно
рассмотреть
эту теорему
при r│R.
Перечень
следствий
можно и
продолжить.
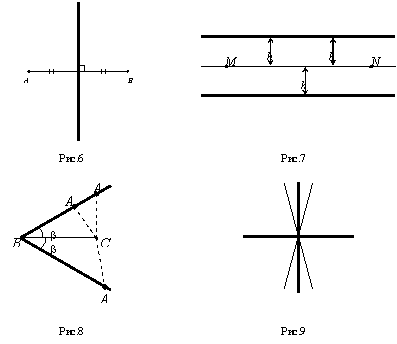
2. ГМТ,
равноудаленных
от двух
данных точек
А и В (от
концов
отрезка АВ),
есть
перпендикуляр
к отрезку АВ,
проходящий
через
середину
этого
отрезка (серединный
перпендикуляр
к отрезку АВ,
или
симметраль
точек А и В)
(рис. 6).
3. ГМТ,
равноудаленных
на
расстояние h
от данной
прямой MN,
есть
совокупность
двух
различных
прямых,
параллельных
MN и
удаленных от
нее на
расстояние h (граница
полосы
шириной 2h с
симметралью MN)
(рис. 7).
4. ГМ
вершин А
треугольников
с общим
основанием
ВС, углом ąАВС=b,
прилежащим к
основанию,
есть
совокупность
двух лучей,
исходящих из
точки В и
составляющих
с основанием
угол b
(рис. 8).
5. ГМТ, расстояния которых до двух данных пересекающихся в точке О прямых относятся как данные отрезки m и n, есть совокупность двух прямых, проходящих через точку О, определенным образом построенных.
 |
6. ГМТ,
из которых
данный
отрезок ВС=а
виден под
данным углом a,
есть
совокупность
дуг двух
сегментов,
построенных
на отрезке ВС
и вмещающих
угол a
(точки В и С
исключаются) (рис.
10а,б,в).
Следствие
1. ГМТ,
из которых
отрезок ВС = а
виден
под прямым
углом, есть
окружность,
построенная
на ВС
как на
диаметре (исключая
точки В
и С) (рис. 10б).
Следствие
2. ГМТ,
из которых
данный
отрезок ВС виден
под углом, не
меньшим, чем a,
есть все
точки двух
сегментов,
построенных
на ВС и
вмещающих
угол a
(исключая
точки В
и С)[1].
Следствие
3. ГМТ,
из которых
данный
отрезок ВС
виден под
углом,
меньшим, чем a, есть все
точки
плоскости,
исключая
точки
предыдущего (следствие
2)
геометрического
места.
7. ГМТ,
расстояния
которых до
двух данных
точек В и С (ВС=а)
относятся
как m
: n,
есть
окружность
Аполлония с
диаметром
![]() ,
где P
и Q ¢
точки,
делящие
отрезок ВС в
отношении m
: n,
соответственно,
внутренним и
внешним
образом.
,
где P
и Q ¢
точки,
делящие
отрезок ВС в
отношении m
: n,
соответственно,
внутренним и
внешним
образом.
Примечание. При m = n окружность Аполлония вырождается в серединный перпендикуляр к ВС (ГМТ 2).
Выясним
существо
метода
геометрических
мест.
Так как мы
имеем дело с
классом
задач,
решаемых
только
циркулем и
линейкой, то
каждую
искомую
точку можно
рассматривать
как
пересечение
или двух
прямых, или
двух
окружностей,
или прямой и
окружности.
Искомая
точка
обладает
двумя
геометрическими
свойствами,
каждое из
которых
относит эту
точку
соответствующему
геометрическому
месту. Эти
свойства
необходимо
усмотреть
исходя из
условия
задачи.
Если
геометрическое
место еще
неизвестно
как
геометрический
образ, то надо
предварительно
решить
вспомогательную
задачу ½об
отыскании
геометрического
места╗.
Каждая
точка,
принадлежащая
одновременно
и тому и
другому
геометрическому
месту, т. е.
каждая общая
обоим местам
точка, может
привести (но
может и не
привести) к
решению.
Решения не
будет, если
общих точек
двух
геометрических
мест не
существует.
Исходя из
этого идея
анализа при
помощи
геометрических
мест кратко
может быть
выражена так.
Указав
искомые
элементы (точки),
устанавливаем
геометрические
свойства
каждого из
них и по этим
свойствам
относим эти
элементы
соответствующим
геометрическим
местам точек.
Существование
элементов,
общих
геометрическим
местам, лишь
необходимо,
но еще
недостаточно
для решения
задачи;
окончательный
ответ дает
этап
исследования.
 В
качестве
примера
проведем
анализ при
помощи
геометрических
мест в
следующих
задачах.Задача
3. Построить
треугольник
по a, b и
углу В=b
при
основании.
В
качестве
примера
проведем
анализ при
помощи
геометрических
мест в
следующих
задачах.Задача
3. Построить
треугольник
по a, b и
углу В=b
при
основании.
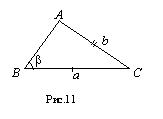
Анализ.
Предположим,
что задача
решена и
треугольник АВС
(рис. 11) ¢
искомый.
Построить
этот
треугольник
можно, если
знать,
например,
положение
всех его
вершин.
Положение
вершин В
и С можно
считать
известным,
тогда
остается
найти точку А.
А ¢
искомая
точка. Чтобы
найти
искомое, надо
знать его
геометрические
вытекающие
из условия
задачи
свойства.
Первое
свойство
точки А: она
является
вершиной
треугольника
с основанием ВС=а
и данным
углом АВС при
основании.
Следовательно,
точка А
принадлежит
ГМТ 4, т. е. лучу ВА
(составляющему
с основанием ВС
угол b)
или лучу ВАó,
являющемуся
образом ВА при
симметрии
относительно
ВС.
Однако
положение
точки А
на плоскости (относительно
точек В
и С) по
одному этому
свойству
найти не
удастся.
Выясним
второе
свойство
точки А.
Оно очевидно:
точка А
удалена от
точки С
на данное
расстояние b, т.
е. А
принадлежит
ГМТ 1 ¢
окружности (С,b).
Вывод.
Если точка А
существует,
то она есть
точка
пересечения
лучей ВА
и ВАó
с
окружностью (С,
b).
План
построения
очевиден.
Задача
4. Построить
окружность,
проходящую
через данную
точку М и
касающуюся
данной
окружности w
в данной ее
точке L.
Анализ.
Предположим,
что задача
решена.
Окружность w1
¢ искомая (рис.
12). Из
определяющих
элементов
окружности w1
¢ точек L и О1
(или М и О1)
¢
неизвестной
точкой,
т. е. искомой, является точка О1.
 Одно
из свойств
точки О1
очевидно:
точка О1
есть центр
окружности,
касающейся
данной
окружности w
в точке L;
поэтому О1╠OL.
Одно
из свойств
точки О1
очевидно:
точка О1
есть центр
окружности,
касающейся
данной
окружности w
в точке L;
поэтому О1╠OL.
Второе
свойство
точки О1:
точка О1
есть центр
окружности,
проходящей
через точки L
и М,
поэтому О1
равноудалена
от этих точек.
Следовательно,
точка О1
принадлежит
серединному
перпендикуляру
к отрезку LM.
Вывод.
Если точка О1
существует,
то она
является
точкой
пересечения
прямой OL
и
серединного
перпендикуляра
к отрезку LM.
[1]
Включая
дугу
сегмента.
Это
следствие
приводится
для того,
чтобы
обратить
внимание на
более или
менее
распространенную
ошибку,
когда под
ГМТ 6
понимают
совокупность
двух
сегментов,
вмещающих
данный угол.